Moore's Law of Moore's Law of Quantum Computing

Classical computers double in power every two years (Moore's Law).  That trend has lead to an explosion in computational power over the last half-century.

Quantum computers, however, may leapfrog that trend by centuries in just the next 20 years.

These complex thinking machines operate at near Absolute Zero and rely on the 'Spooky' properties of entangled particles.  Imagine STAR TREK levels of technology arriving by the 2040's.  

But it all hinges on solving one engineering challenge...

Moore's Law

Since 1949, the power of digital computers has grown exponentially. The trajectory of this growth is known as "Moore's Law".

First proposed by Intel Co-Founder & CEO Gordon Moore in 1965, Moore noticed that the number of transistors on an integrated circuited seemed to double at regular intervals.

In 1975, Moore predicted that computational power would double every 2 years for the foreseeable future.

Moore's prediction has held accurate to present day. It is now is colloquially called a 'Law'.

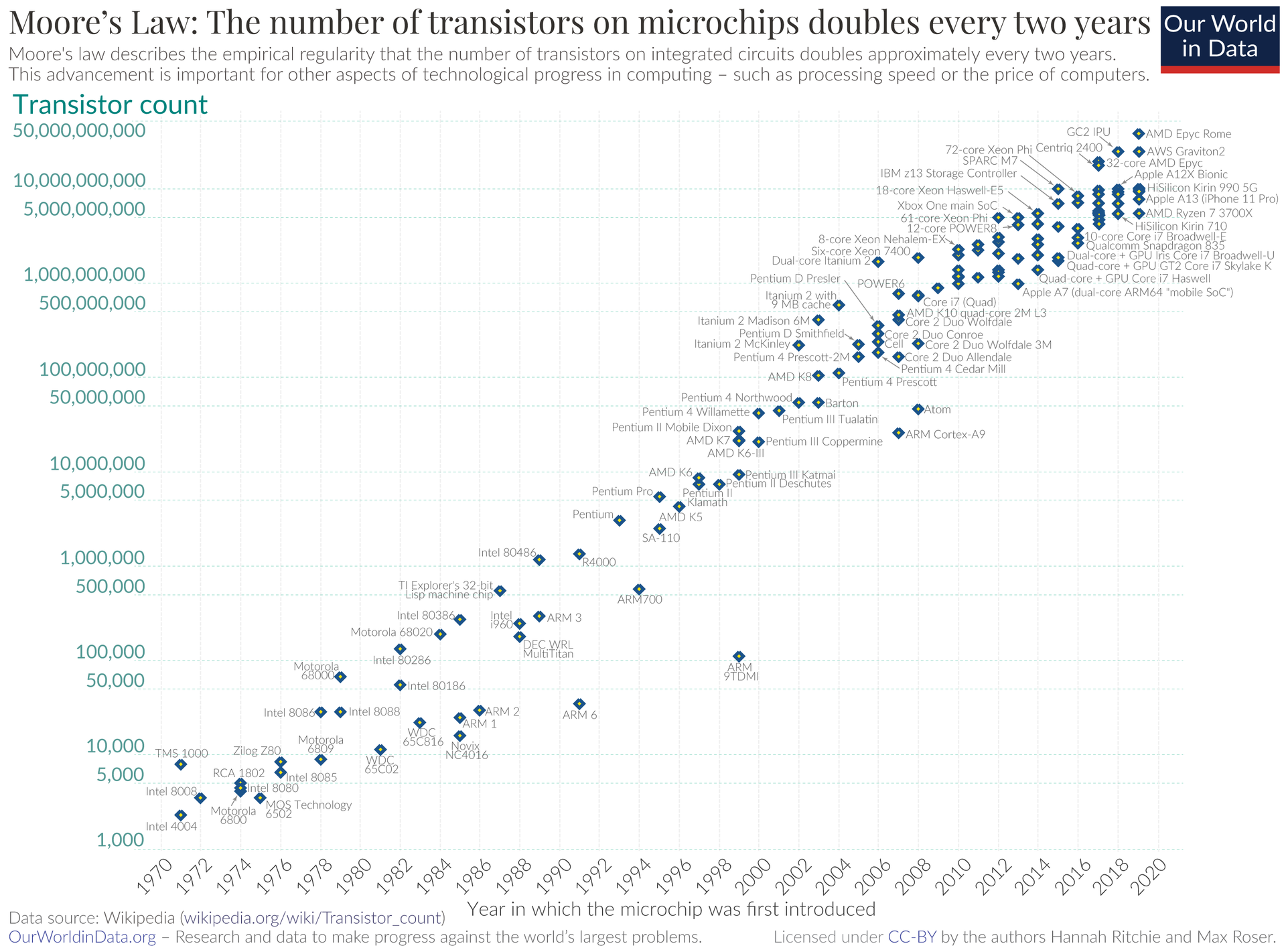
Of course if something doubles at a regular interval, it's growth is exponential.  

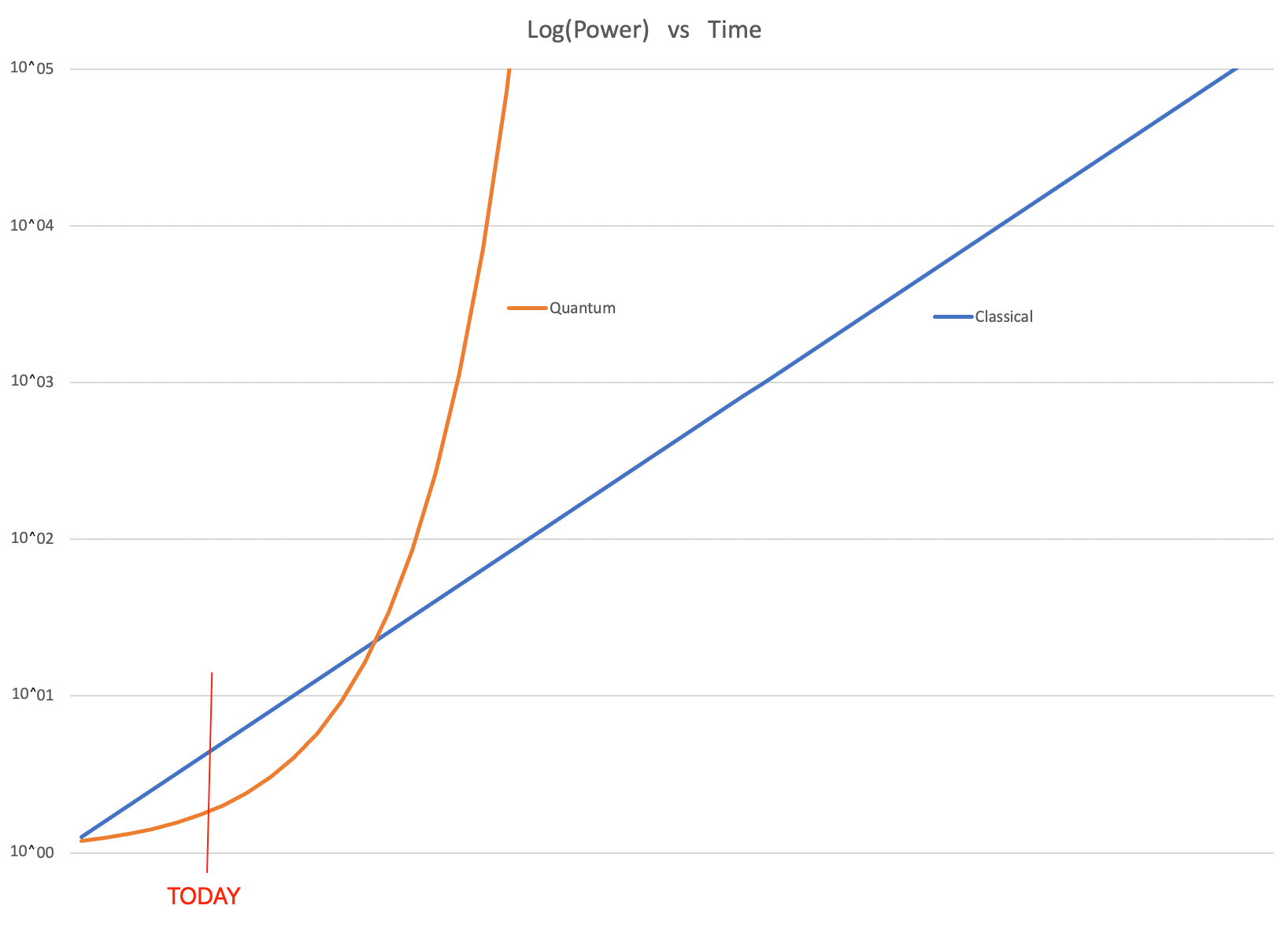
Typically, examples of exponential growth are shown on a Logarithmic-Scale like the scatter plot above. Logarithmic scale displays exponential growth as a straight line.

Several other aspects of computer technology follow Moore's Law/Exponential growth as well, including:

• Memory
• Network connection speeds
• Megapixels
• RAM & flash

As of 2021, this trend is likely to continue for at least a few more years.  

Beyond that, integrated circuits are limited by the atomic scale and issues of electron tunneling.

Enter Quantum Computing...

Quantum Computers

Here is IBM's 53-Qubit Quantum Computer, the cutting edge of this powerful new technology.

These machines are expanding the universe of what's possible in computation.  For certain specialized tasks, quantum computers are already 100 Trillion times faster than conventional super computers.

To understand what makes quantum technologies so powerful, we must start with the basic units of information.

The Bit

In traditional electronics, the fundamental unit of computation is the Bit.  The bit is represented as either 0 or 1.  

Any electronic component holding one of two possible states is said to store 1 bit of information.  Examples include an electric current at either high or low voltage, or a gate which is either open or closed.

Bits are discrete and they are known.

The Qubit

The quantum counterpart to the bit, is called the Qubit (pronounced "Q - Bit").

Qubits have strange and wonderful properties.  They can be both 0 and 1 at the same time, a property known as Quantum Superposition.

Crucially, qubits can enter into Entanglement with other qubits.  For example if two qubits are both equal to 1 and their states are entangled, by flipping one qubit to 0 the other qubit flips as well.

Complexity

This may not feel especially powerful, but the implications get more complex when logic gates are combined with entanglement & superposition...

(Don't worry if the next part loses you...)

Two qubits, which are both in a superposition of 0 and 1 and not entangled, pass through an AND gate  acting on a third qubit.  The three qubits are now entangled with the first two maintaining independent 25% probabilities of 00, 01, 10 and 11, while the third qubit is 1 when the two inputs are  11, but is 0 in the other three states...

What if we keep stacking these gates and entanglements until a useful algorithm is produced?

By starting with a superposition of all possible inputs, the algorithm calculates the entire search space of the problem in just one iteration!

(This is not easy to imagine... just trust me on the messy bits.)

Parallel Dimensions

Where do the special properties of quantum machines come from?

Most physicists and quantum computing experts tend toward a multiverse explanation of reality.  

The circuit's qubit exists in an infinite number of almost identical worlds.  The quantum computer allows the operator to reach across dimensions and manipulate qubits in infinite worlds, before observing the output.

That final act of observation actually collapses you the observer to one of the possible dimensions. Or more specifically, to a subset of the dimensions...

(Okay okay... that's the last heavy/weird stuff)

Making a comparison

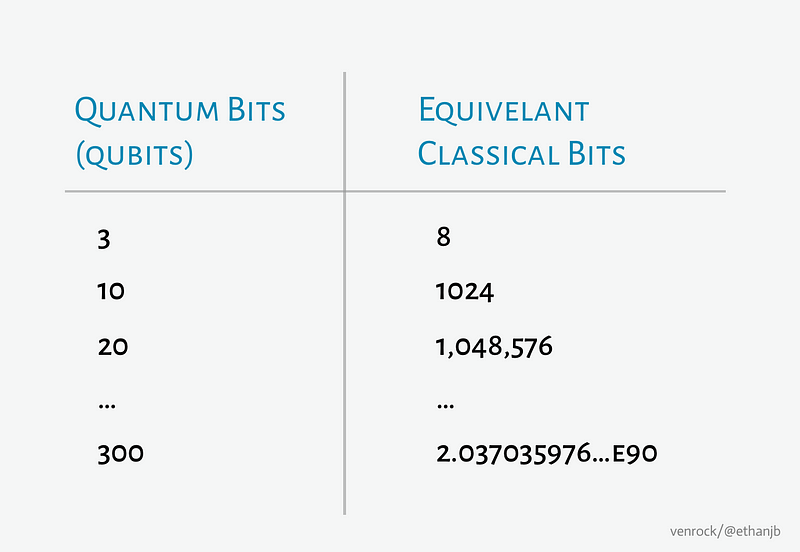
Qubits are like exponentially powerful Bits.

A good rule of thumb when comparing the power of classical & quantum computers: Bits = 2^Qubits

A qubit can do any computation a normal bit can do, but it can compute every version of the inputs in only one cycle of the algorithm.  

Since N bits can represent 2^N combinations, N qubits can search 2^N versions of an algorithm in one cycle.

Algos & Errors

This rule of Bits = 2^Qubits isn't exactly correct.  Qubits are more sensitive to corruption than normal bits.

Four years ago, I was fortunate enough to spend some time on IBM's quantum computer.  I designed quantum circuits and saw first-hand how errors occur and compound in the fragile ultra-cryogenic environment.

Later, I will discuss some of the limits and technical challenges to modern quantum computers.  

For right now, however, I'm going to ignore these complicating factors and assume our quantum computers have no noisy errors.

Moore's Law of Moore's Law: Rose's Law

Let's revisit that formula again: Bits = 2^Qubits

One implication is that to double the power a quantum computer, just add 1 Qubit.

Therefore to keep pace with Moore's Law, quantum machines need only grow by 1 qubit every 2 years.

So how are Qubits vs Time progressing?

It turns out that Qubits, like bits or transistors, are increasing at an exponential rate.

I ran a regression on the doublings in qubits and found they 2x every 5 years with 1989 as year zero.  

Remember in Moore's Law transistors 2x every 2 years with 1949 as the starting point.

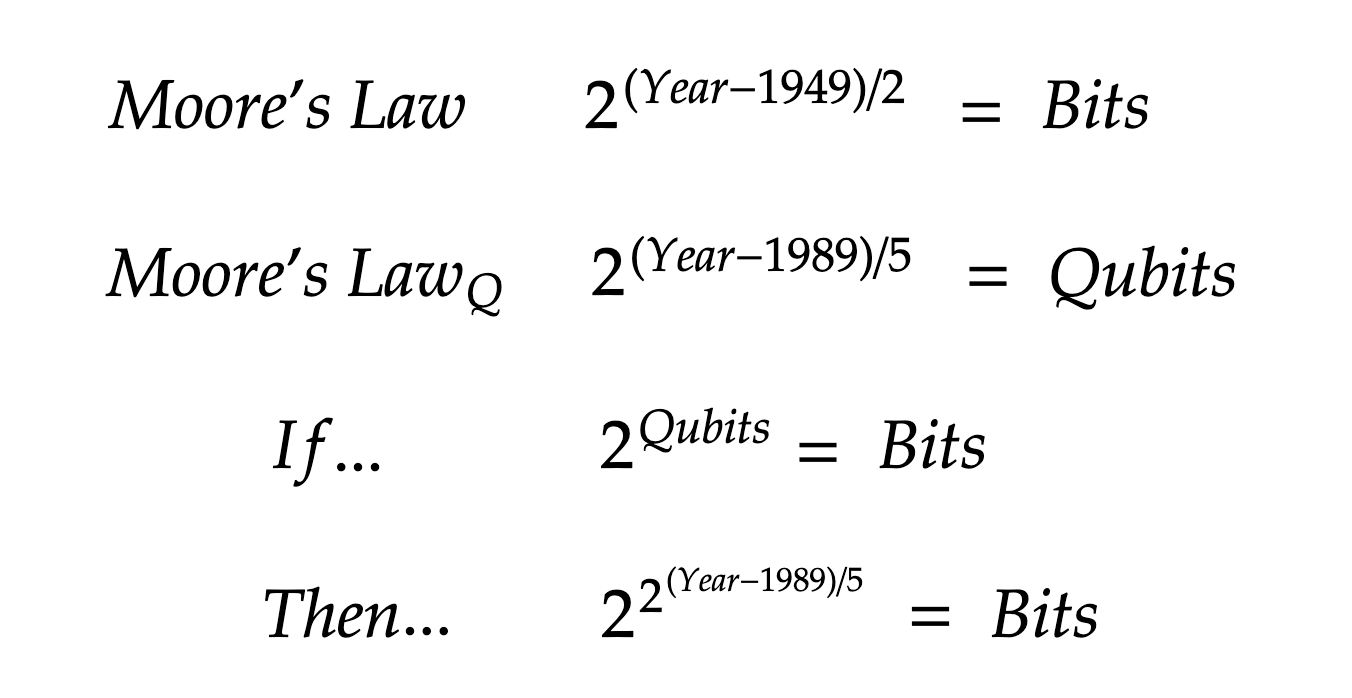
This meta-Moore's Law is known as "Rose's Law" after D-Wave Co-Founder & Former CEO Geordie Rose.  

The term "Rose's Law" was coined by D-Wave early investor Steve Jurvetson.

This exponential exponential growth is where it all really diverges...

Exponents & Logarithms

Classical computers increase in power exponentially.  On a logarithmic scale this appears as a straight line.

Quantum computers appear as an Exponential function on the same Log-Scale.

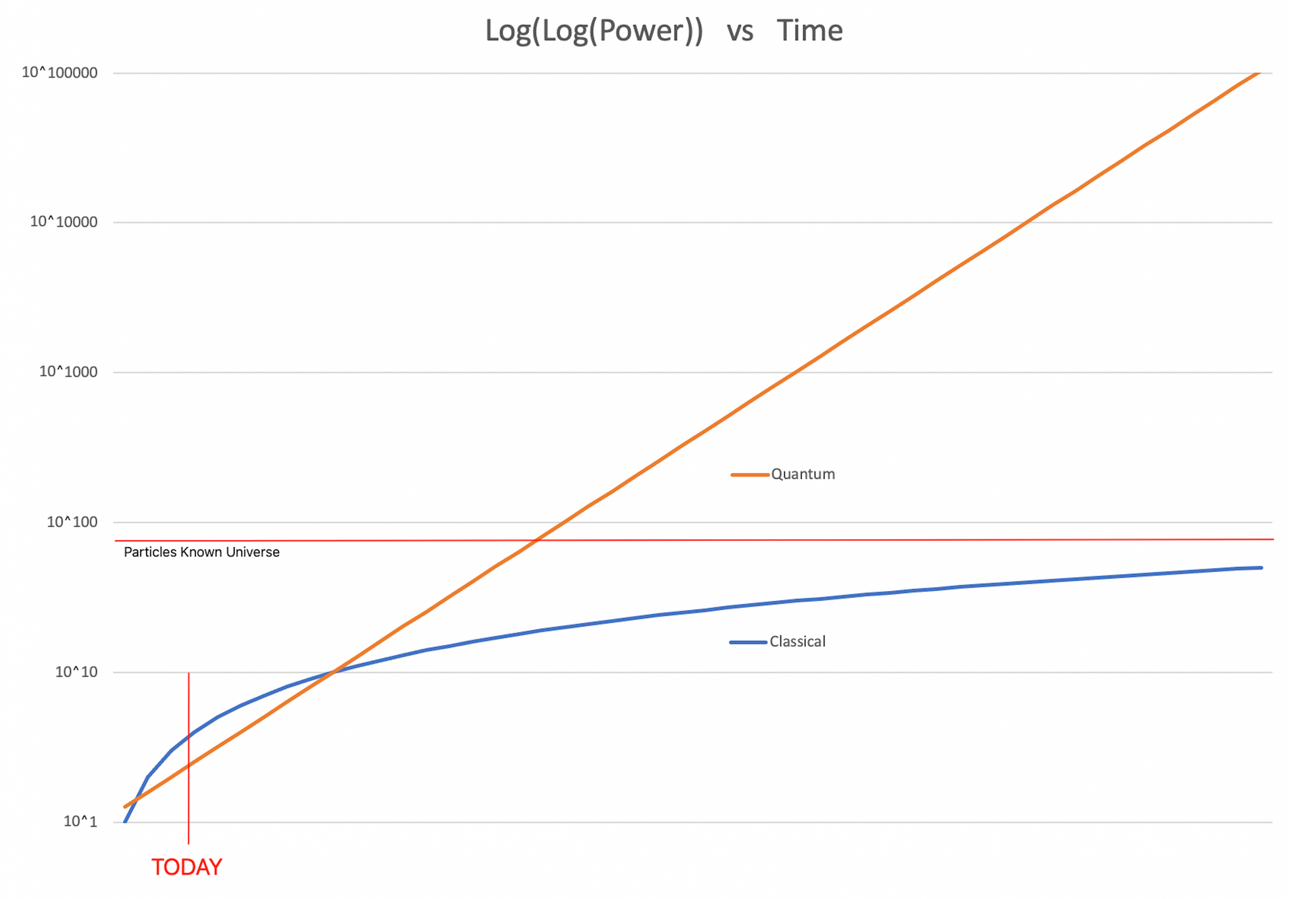
It's only on a Log(Log)-Scale that quantum computation is Linearized.

Deep Sci-Fi

Imagine the absolute most powerful (classical) computer that could be built…

Precision: Every transistor or gate is made from only a single atom.

Scale: All the matter of the entire universe is consumed to build this Goliath Machine.

Forget that 99.9% of the atoms in the universe are hydrogen or helium.  We've rearranged the subatomic particles to make more useful elements for the computer.

Also don't worry that this machine would be tens of thousands of lightyears in each direction slowing the circuits to that effective speed (20,000 years to send 1 signal).  That has been fixed as well (some how).

We will imagine this absolute limit of computers, without any practical constraints.

How far into the future would Moore's Law have to extrapolate for this Goliath Machine to come into existence?

Given the formula above for Moore's Law and an estimated 10⁸⁰ atoms in the universe, this computer would hit the market sometime around July 2480.

What about a computer a TRILLION TRILLION TRILLION times more powerful than the Goliath Machine?

Moore's Law tells us that would take an additional 239 years, or around the Year 2719.

This is starting to evoke Isaac Asimov...

Quantum Singularity

However, with the current progression of Quantum Computing, the Goliath Machine would available in 2040. Furthermore, since it's a quantum machine it would only occupy about 1 cubic meter.

What about the Goliath Machine x TRILLION TRILLION TRILLION?

That wouldn't be available for another 9.5 months.

This sort of extrapolation of technologies might seem outrageous.  But remember that only 33 years separated the Wright Brothers' Flyer from the first jet aircraft.  And only 33 years separated the first jet from the Moon Landing.

Imagine attempting to extrapolate classical (chemical) bombs around 1944 and then discovering nuclear weapons?  

Or 7 years later, when thermonuclear weapons raised that by another factor of 1,000-fold...

Quantum leaps in technology do occur.

Applications

What are the applications of such computational technology?  

Beyond a certain point, does a fast computer even affect the real world?

The economy and practical problems?

For some problems, quantum excels brilliantly, in others it's a waste of effort.

Quantum > Classical

Quantum machines, excel at searching all possible inputs or doing optimization within constraints.

Obvious applications include code-breaking (RSA), AI optimization, and Quantum Chemistry.

(RSA is the encryption basis of the Internet. Quantum can break it.)

Molecules are quite difficult for classical computers to model accurately.  The complexity of a molecule grows exponentially with the number of atoms.

This sort of exponential complexity quickly exceeds classical machines' abilities.

However, for a quantum computer, there is a linear relationship between atoms in a molecule and qubits required to model.

Classical > Quantum

Classical computers are the clear winner when the tasks are parallel or sequential.

The best quantum computer in 2050 could never compete with a cheap graphics card today.  For GPUs the calculation inputs are known and calculated in parallel for millions of pixels.

There is no search or optimization here.

Likewise a computation that is sequential, with lots of simple steps (think spreadsheet software), won't offer any special benefits to a quantum algorithm.

Perhaps I'm wrong, but I doubt quantum computers will ever be a common PC.  They will get faster and cheaper. But I imagine them more like servers or DNA sequencers.  Their use will be semi-concentrated to corporate needs.

Physical Applications

Although quantum computers will never become gaming rigs, their impact will not be relegated to encryption or abstract maths either.  There are serious real world needs.

Classical computers are quite bad at modeling physical materials and predicting their behavior. Even a simple 3-atom water molecule is a difficult challenge for a modern supercomputer.

If you are trying to invent nano-materials 10,000x stronger than steel or discover a novel cancer therapy, the chemistry becomes much more complex.

For a taste of the combinatorics of organic molecules, I recommend Isaac Asimov's 1957 essay "Hemoglobin and the Universe".

Hemoglobin, that life-giving carrier of oxygen, which creates our blood's red hue, is a behemoth unto itself.  With over 10,000 atoms arranged into four inter-looped chains, each chain made of helixes as its links, each helix a complex lattice of organic proteins, hemoglobin has one shape when ferrying oxygen and a different shape when not...  

Hemoglobin is a miniature organic machine and it is far from the largest organic molecule...

Star Trek

Quantum computers are perfectly suited to problems of protein-folding, drug research, nano-technology and cutting edge physics.

Combined with innovative engineering, these inter-dimensional cryogenic thinkers may well create a Star Trek future of sorcery-like technologies, yet undreamed of super materials, and eradication of all disease...

So what is the chasm that separates us from a "Where no man has gone before" Star Trek future?

I hinted at the beginning of the article that this "all hinges on solving one engineering challenge..."

Three Challenges

Three challenges are necessary to realize the full potential of quantum:

• More qubits
• Efficient quantum algorithms
• Reduce error rates

Up to this point, we've focused on qubit growth (Problem #1).  

The other challenges include creating good algorithms/circuits/programs and reducing the noise/errors in quantum systems.

On the quantum algorithm frontier, we have a secret weapon!  

Small quantum computers (less than 30 qubits) can be simulated by classical computers. This allows researchers to test circuits and research on a mere personal computer.

Counterintuitively, good quantum algorithms existed before a 1-qubit computer was ever built! (Problem #2)

The real challenge is Problem #3: Reduce Errors/Noise

Cryogenics

Quantum computers operate in the cleanest, coldest, most Entropy-free environments on Earth.

The components require atoms so immobile and static, that the computer can control the spin-orientation of a single electron.

Further, the computer must transfer that state to affect some other particle or relate two particles' orientation to a third (Logic Gate).

Each of these steps attempt to manipulate a particle 10,000,000,000 times smaller than the width of a human hair.  Errors, heat and noise are part of reality.

Currently the error rate on the best quantum computers is ~1% for each elementary operation.

Error Correction

Although 99% accuracy is high, a single mistake can affect the whole entangled system.  One error completely corrupts the result.

There are ways to make a quantum circuit more robust without improving that 1% error value.

As an example, imagine a small part of your overall circuit.  This unit needs several elemental operations to complete it's task.  With each operation, the 1% chance of error compounds.

The overall unit an error rate of 5%.

One way to improve this error: Replicate 3 identical copies of the unit and have them vote on the output.

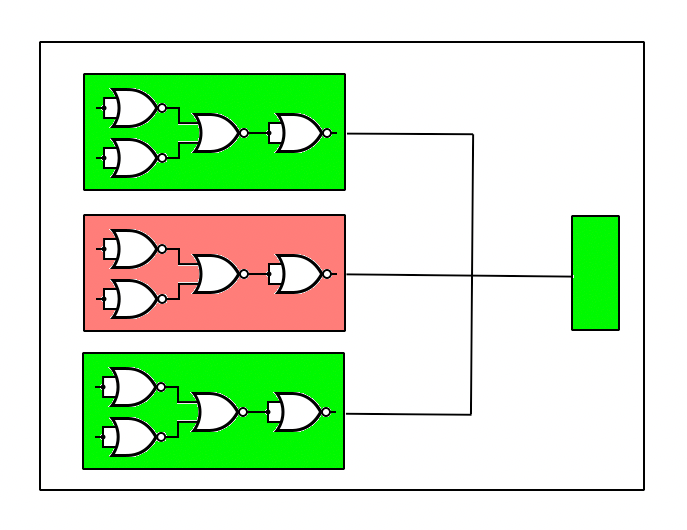
This meta-unit can still give erroneous answers, but only when 2 or all 3 of the units are in error.

This reduces the over error rate to 0.72% for the unit.

Of course there would also be new bits of circuit which measure the votes.  This step introduces some error as well...

For simplicity, let's assume that the 2-of-3 circuit with the vote measurement has an error rate of 2%.

That's an improvement in accuracy at the cost of tripling the circuit size. Probably closer to 3.5x including the vote-counting.

Nested Structures

As the complexity of the circuit grows and errors increase, soon another layer of 2-of-3 voting is needed.

Though here each of the subcomponents is a meta-circuit itself.

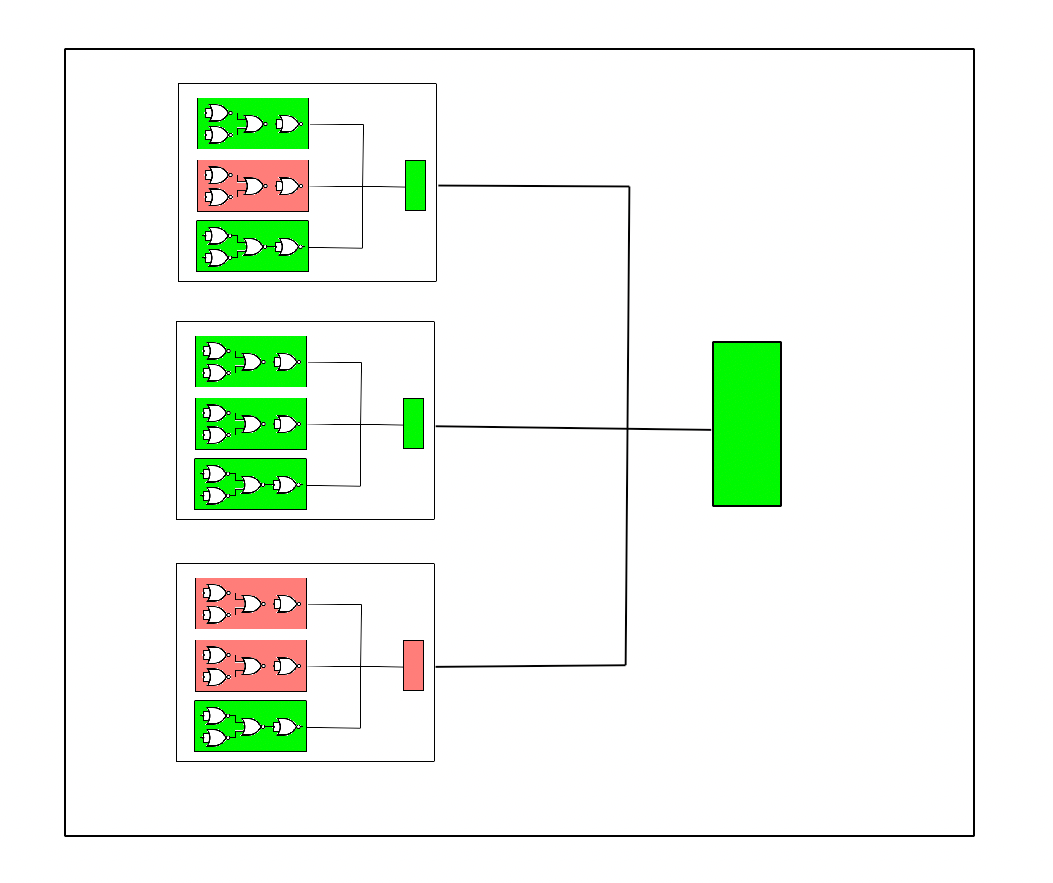
More complex circuits and further layers of error reduction require the number of qubits to grow exponentially.  With enough complexity you just can't get ahead.

Google estimates that current technology requires 1,000 physical qubits to encode 1 logical qubit with an accuracy of 1-in-one billion.  That's a rough trade-off.

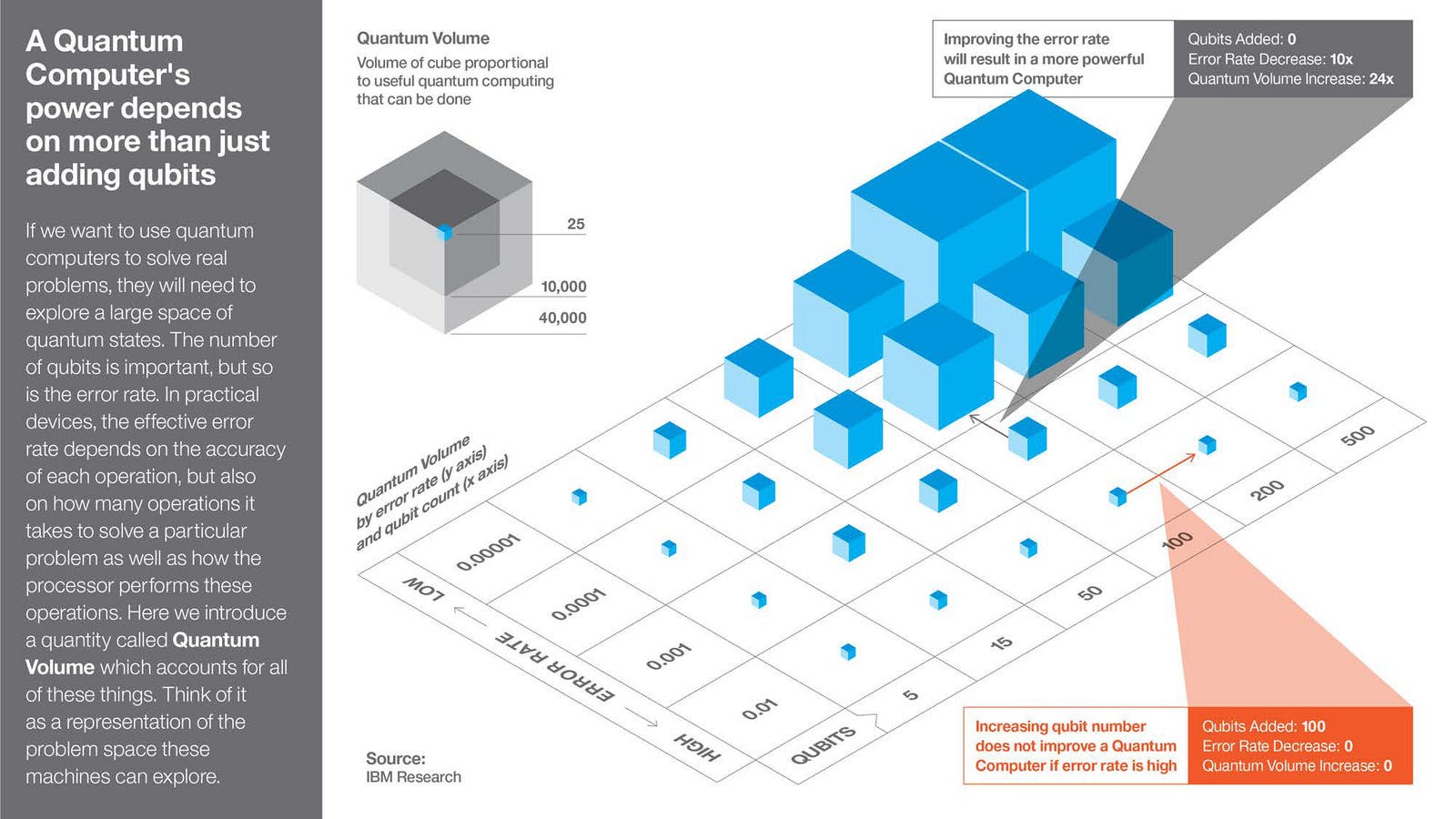
At this point in the development of quantum computers, almost all of the advancement in technology relies on improving the errors rates.

This is the most important challenge!

Conclusion: To move the fulcrum...

"Give me a lever long enough and a fulcrum strong enough, and I will move the world" - Archimedes-

Archimedes knew that even a single human could lift something massive if the fulcrum was correctly placed.

I imagine the Error Rate in quantum machines to be something akin to a Fulcrum placed between Archimedes and Massive Computation.

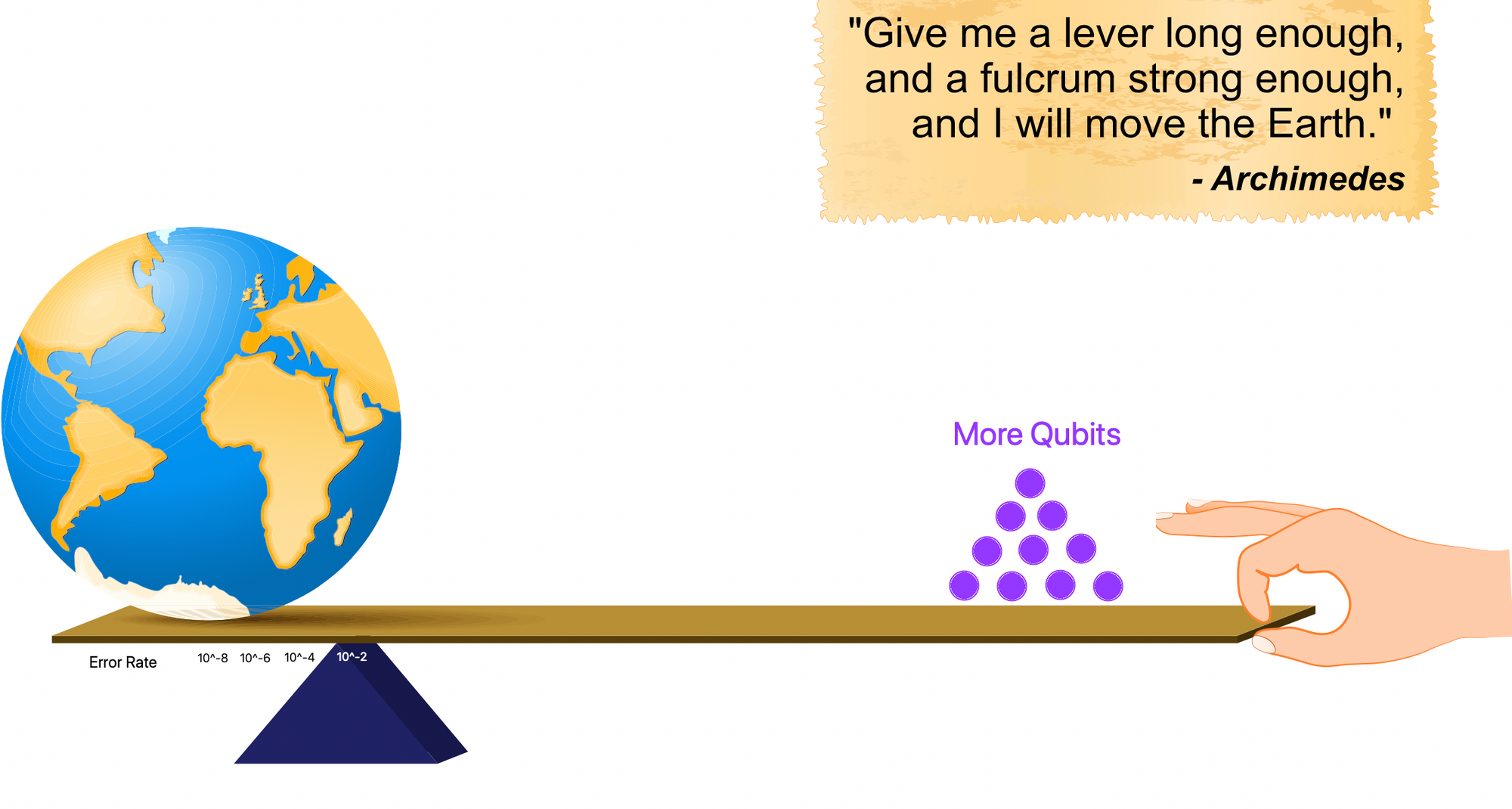
On one side, our Greek mathematician is patiently stacking shinny qubits.  The other side holds our world, rising toward a Star Trek future.

Whether or not we rise toward the stars, depends on how far we can move the Error Rate.

Small improvements in the error rate will result in massive advances in computing.

Current quantum machines (1-in-100 errors) are vaguely useful in some toy problems.

At 1-in-10,000 errors, these machines could revolutionize medical research, materials engineering and encryption (Goodbye RSA Internet).

That future hinges entirely on solving one engineering challenge: Error Rates

If tomorrow a start-up announces Q-Gates with transistor-like stability (1-in-1 Billion) are in production, then you should get very excited!

We will be aboard the Starship Enterprise in this century...

-Nick Yoder- @NickYoder86

Special Thanks to Steve Jurvetson for his contributions.