A Mathematical Constraint on Reality: Why the Universe Must Be 11-Dimensional

I believe I’ve found a structural limit on what dimensions can host physical law — and it emerges not from speculative metaphysics, but from concrete, computational logic.

This isn’t just a hunch. It’s a kind of mathematical quasi-proof — one that starts with a deceptively simple observation:

Every physical process must be mathematically possible. But not every mathematical object can manifest physically.

From this axiom, I arrive at a startling implication: physical reality can only exist in 1, 3, and 7 dimensions, totaling 11 when you include time, space, and “hidden” structure. Remarkably, this aligns with M-theory, the most ambitious unifying theory in physics. But my path there didn’t start with string theory. It started with the cross product.

All Physical Processes Must Be Mathematically Possible — But Not Vice Versa

Not every mathematical structure manifests in physical reality. The universe is under no obligation to realize all that is mathematically consistent. But the reverse is absolutely true:

If something occurs in the physical world, it must be mathematically definable.

Every physical interaction — from gravity to electromagnetism to the spin of a particle — must be encoded in a structure that supports it computationally. If there's no underlying math that allows it to happen, then it can't happen. This is not philosophy. It’s a boundary condition for consistency in physics.

Binary Cross Product Only Exists in ℝ⁰, ℝ¹, ℝ³, and ℝ⁷

The vector cross product is an elegant operation:
Given two vectors, it produces a third vector that is:

• Orthogonal to both
• Has a magnitude equal to the area of the parallelogram they span
• Follows a consistent handedness (orientation)

Recently, I was surprised to learn that this binary vector cross product, only exists in a few dimensions:

n=0, 1, 3, 7

This operation — so essential to physics — only exists in four specific dimensionalities.

This is not arbitrary. It’s a hard result from algebraic topology (Adams’ theorem) and deeply tied to the structure of normed division algebras — the real numbers ℝ, complex numbers ℂ, quaternions ℍ, and octonions 𝕆 — which exist only in dimensions 1, 2, 4, and 8, respectively. Their imaginary parts, where cross products live, are precisely dimensions 0, 1, 3, and 7.

Physical Operations Like Torque, Angular Momentum — and the Flow of Time — Require These Dimensions

Many fundamental physical quantities rely on the existence of a binary cross product.

In ℝ³ (3D Space), this gives us:

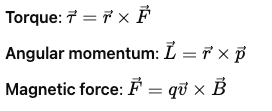
These are not possible in dimensions like ℝ⁴ or ℝ⁶. In those spaces, the orthogonal complement to two vectors doesn't yield a unique perpendicular vector. The output of a “cross product” becomes a subspace, not a direction. As a result, any such force would be diffuse and undefined, with no observable behavior.

In ℝ¹ (Time), valid operations also exist — and are just as important.

In one dimension, only addition and inversion are well-defined operations — and that’s exactly what time supports.

Time’s one-dimensionality ensures a linear order of causality, irreversible entropy, and bounded propagation of information. If time were multi-dimensional, these core features of physics would collapse.

So I see dimensions 1 (time), 3 (space), and 7 (hidden) as not just useful — they are computationally required.

Total of 11 Dimensions: 1 (Time) + 3 (Space) + 7 (Other)

Here’s where the shock hit me.

If only 1, 3, and 7-dimensional spaces support physically consistent vector products and causal action, then physical reality is computationally constrained to exactly these dimensions. That adds up to:

1 (time)+3 (observable space)+7 (internal structure)=11 total

This matches M-theory’s prediction precisely: an 11-dimensional universe with 7 compactified spatial dimensions and 4 large ones (3 space + 1 time).

But I didn’t arrive at this via M-theory (mathematician, not a physicist). I arrived by tracking which dimensions can support directional, causal, and observable physical interactions — and 11 is the only total that fits.

Addendum: Why Other Dimensions (May) Exist — But Cannot Manifest Physically

It’s tempting to ask: why not 4, 5, or 6 dimensions? Aren’t those also vector spaces?

Mathematically, yes. Physically, no — because of one key fact:

In those dimensions, the orthogonal complement to two vectors is not one-dimensional — it’s a higher-dimensional subspace. So any output vector from a physical interaction is not unique.

And in quantum mechanics, uniqueness matters. According to the Born Rule, the probability of observing a quantum state is the square of its projection amplitude. If a process produces an entire continuum of equally valid outputs, the probability of observing any single one is effectively zero.

So in ℝ⁴, ℝ⁵, or ℝ⁶, the “spread” of possible outcomes kills observability. The only dimensions where observable physical vectors resolve uniquely are 1, 3, and 7.

In other words: the other dimensions may exist mathematically, but they are always observed with probability 0. Effectively non-existant.

Conclusion

I started by trying to understand why torque and angular momentum — so central to physics — only make sense in three dimensions, but stumbled upon a structural constraint on all of reality.

Binary cross products — and the kinds of causality and symmetry they enable — only exist in dimensions 1, 3, and 7. These are the only spaces where observable forces can act cleanly, where nature can compute cause and effect without ambiguity, and where physical law can actually resolve into outcomes.

That totals 11 dimensions. Time. Space. And the strange, silent symmetry of ℝ⁷.