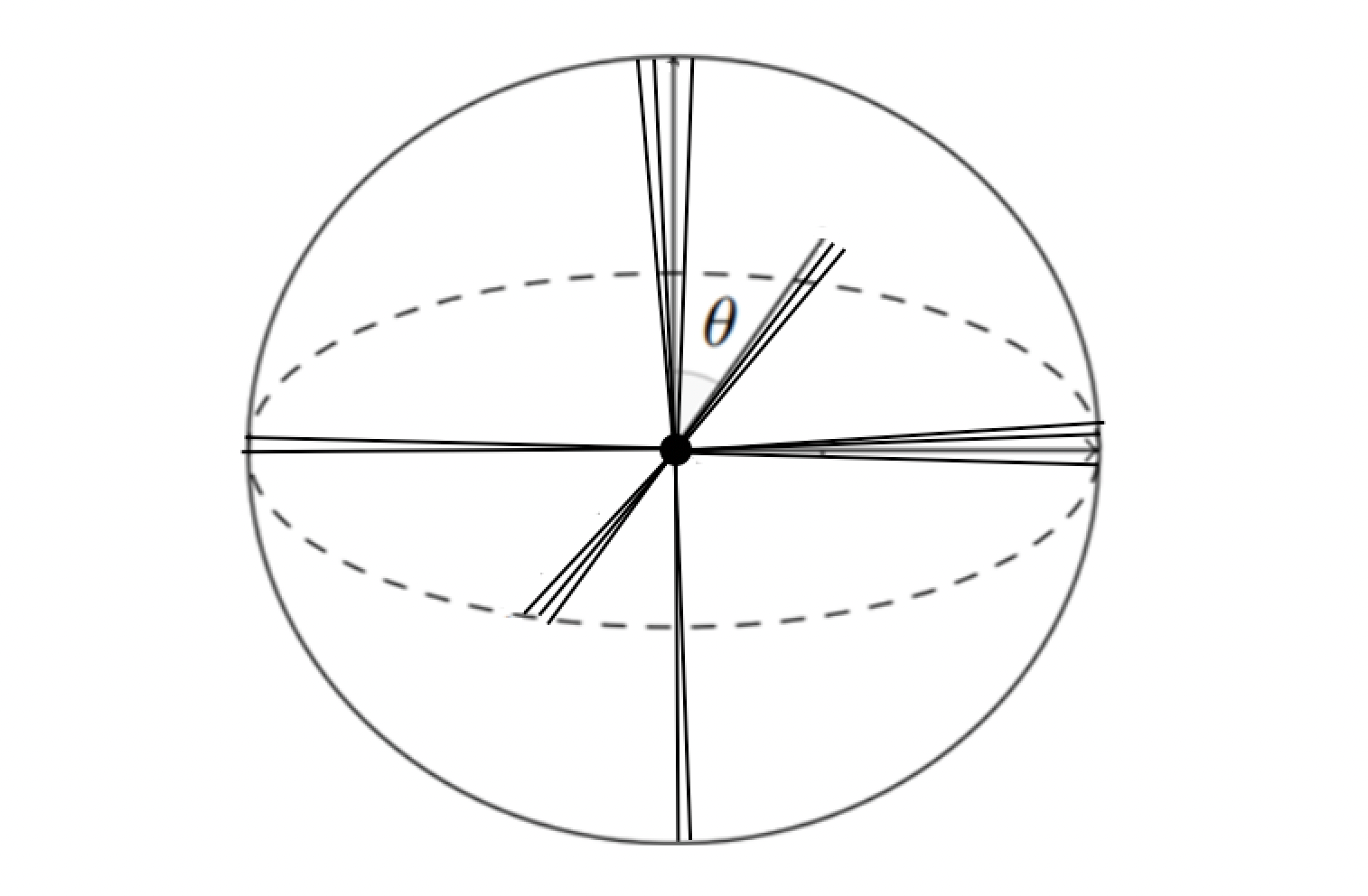
In a recent 3Blue1Brown video series on transformer models, Grant Sanderson posed a fascinating question: How can a relatively modest embedding space of 12,288 dimensions (GPT-3) accommodate millions of distinct real-world concepts?

The answer lies at the intersection of high-dimensional geometry and a remarkable mathematical result known as the Johnson-Lindenstrauss lemma. While exploring this question, I discovered something unexpected that led to an interesting collaboration with Grant and a deeper understanding of vector space geometry.

The key insight begins with a simple observation: while an N-dimensional space can only hold N perfectly orthogonal vectors, relaxing this constraint to allow for "quasi-orthogonal" relationships (vectors at angles of, say, 85-95 degrees) dramatically increases the space's capacity. This property is crucial for understanding how language models can efficiently encode semantic meaning in relatively compact embedding spaces.

In Grant's video, he demonstrated this principle with an experiment attempting to fit 10,000 unit vectors into a 100-dimensional space while maintaining near-orthogonal relationships. The visualization suggested success, showing angles clustered between 89-91 degrees. However, when I implemented the code myself, I noticed something interesting about the optimization process.

The original loss function was elegantly simple:

loss = (dot_products.abs()).relu().sum()

While this loss function appears perfect for an unbounded ℝᴺ space, it encounters two subtle but critical issues when applied to vectors constrained to a high-dimensional unit sphere:

1. The Gradient Trap: The dot product between vectors is the cosine of the angle between them, and the gradient is the sine of this angle. This creates a perverse incentive structure: when vectors approach the desired 90-degree relationship, the gradient (sin(90°) = 1.0) strongly pushes toward improvement. However, when vectors drift far from the goal (near 0° or 180°), the gradient (sin(0°) ≈ 0) vanishes—effectively trapping these badly aligned vectors in their poor configuration.
2. The 99% Solution: The optimizer discovered a statistically favorable but geometrically perverse solution. For each vector, it would be properly orthogonal to 9,900 out of 9,999 other vectors while being nearly parallel to just 99. This configuration, while clearly not the intended outcome, actually represented a global minimum for the loss function—mathematically similar to taking 100 orthogonal basis vectors and replicating each one roughly 100 times.

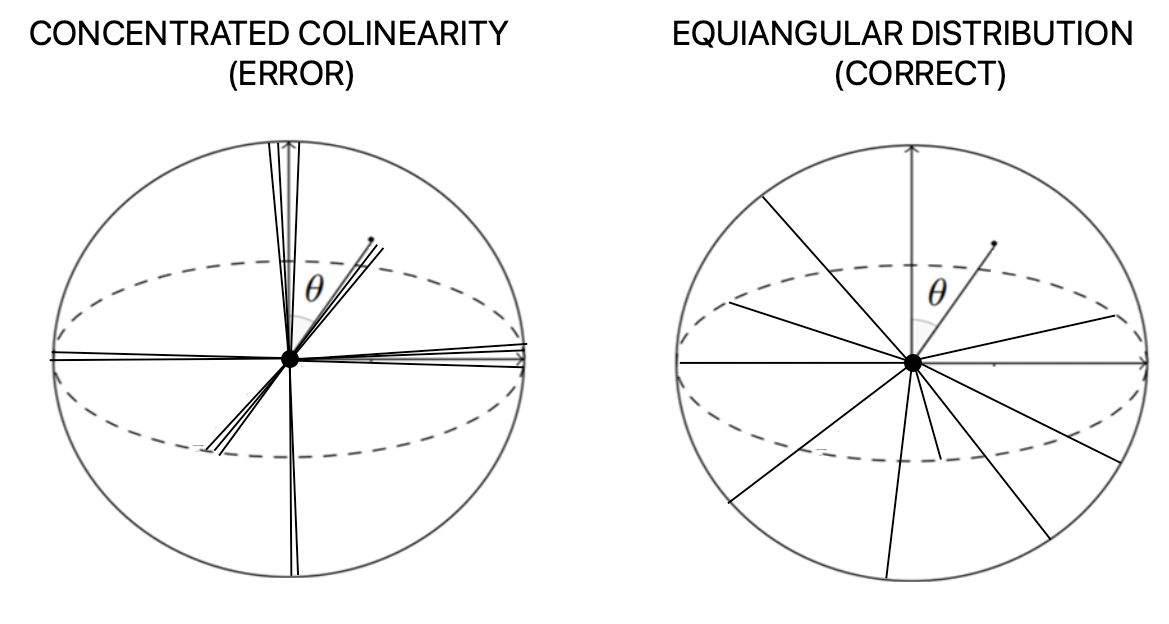
This stable configuration was particularly insidious because it satisfied 99% of the constraints while being fundamentally different from the desired constellation of evenly spaced, quasi-orthogonal vectors. To address this, I modified the loss function to use an exponential penalty that increases aggressively as dot products grow:

loss = exp(20*dot_products.abs()**2).sum() (Full code here)

This change produced the desired behavior, though with a revealing result: the maximum achievable pairwise angle was around 76.5 degrees, not 89 degrees.

This discovery led me down a fascinating path exploring the fundamental limits of vector packing in high-dimensional spaces, and how these limits relate to the Johnson-Lindenstrauss lemma.

When I shared these findings with Grant, his response exemplified the collaborative spirit that makes the mathematics community so rewarding. He not only appreciated the technical correction but invited me to share these insights with the 3Blue1Brown audience. This article is that response, expanded to explore the broader implications of these geometric properties for machine learning and dimensionality reduction.

The Johnson-Lindenstrauss Lemma: A Geometric Guarantee

At its core, the Johnson-Lindenstrauss (JL) lemma makes a remarkable promise: you can project points from an arbitrarily high-dimensional space into a surprisingly low-dimensional space while preserving their relative distances with high probability. What makes this result particularly striking is that the required dimensionality of the low-dimensional space grows only logarithmically with the number of points you want to project.

Formally, the lemma states that for an error factor ε (between 0 and 1), and any set of N points in a high-dimensional space, there exists a projection into k dimensions where for any two points u and v in the original space, their projections f(u) and f(v) in the lower dimensional space satisfy:

(1 - ε)||u - v||² ≤ ||f(u) - f(v)||² ≤ (1 + ε)||u - v||²

The number of dimensions (k) required to guarantee these error bounds is given by:

k ≥ O(log(N)/ε²)

The "Big O" notation can be replaced with a concrete constant C:

k ≥ (C/ε²) * log(N)

Where:

• k is the target dimension
• N is the number of points
• ε is the maximum allowed distortion
• C is a constant that determines the probability of success

While most practitioners use values between 4 and 8 as a conservative choice for random projections, the optimal value of C remains an open question. As we'll see in the experimental section, engineered projections can achieve much lower values of C, with profound implications for embedding space capacity.

The fascinating history of this result speaks to the interconnected nature of mathematical discovery. Johnson and Lindenstrauss weren't actually trying to solve a dimensionality reduction problem – they stumbled upon this property while working on extending Lipschitz functions in Banach spaces. Their 1984 paper turned out to be far more influential in computer science than in their original domain.

From Theory to Practice: Two Domains of Application

The JL lemma finds practical application in two distinct but equally important domains:

1. Dimensionality Reduction: Consider an e-commerce platform like Amazon, where each customer's preferences might be represented by a vector with millions of dimensions (one for each product). Direct computation with such vectors would be prohibitively expensive. The JL lemma tells us we can project this data into a much lower-dimensional space – perhaps just a thousand dimensions – while preserving the essential relationships between customers. This makes previously intractable computations feasible on a single GPU, enabling real-time customer relationship management and inventory planning.
2. Embedding Space Capacity: This application is more subtle but equally powerful. Rather than actively projecting vectors, we're interested in understanding how many distinct concepts can naturally coexist in a fixed-dimensional space. This is where our experiments provide valuable insight into the practical limits of embedding space capacity.

Let's consider what we mean by "concepts" in an embedding space. Language models don't deal with perfectly orthogonal relationships – real-world concepts exhibit varying degrees of similarity and difference. Consider these examples of words chosen at random:

• "Archery" shares some semantic space with "precision" and "sport"
• "Fire" overlaps with both "heat" and "passion"
• "Gelatinous" relates to physical properties and food textures
• "Southern-ness" encompasses culture, geography, and dialect
• "Basketball" connects to both athletics and geometry
• "Green" spans color perception and environmental consciousness
• "Altruistic" links moral philosophy with behavioral patterns

The beauty of high-dimensional spaces is that they can accommodate these nuanced, partial relationships while maintaining useful geometric properties for computation and inference.

Empirical Investigation of Embedding Capacity

When we move from random projections to engineered solutions, the theoretical bounds for C of the JL lemma become surprisingly conservative. While a Hadamard matrix transformation with random elements can reliably achieve a C value between 2.5 and 4 in a single pass, our GPU experiments suggest even more efficient arrangements are possible through optimization.

To explore these limits, I implemented a series of experiments projecting standard basis vectors into spaces of varying dimensionality. Using GPU acceleration, I tested combinations of N (number of vectors) up to 30,000 and k (embedding dimensions) up to 10,000, running each optimization for 50,000 iterations. The results reveal some fascinating patterns:

Several key observations emerge from this data:

1. The value of C initially rises with N, reaching a maximum around ~0.9 (notably always below 1.0)
2. After peaking, C begins a consistent downward trend
3. At high ratios of N to K, we observe C values trend below 0.2

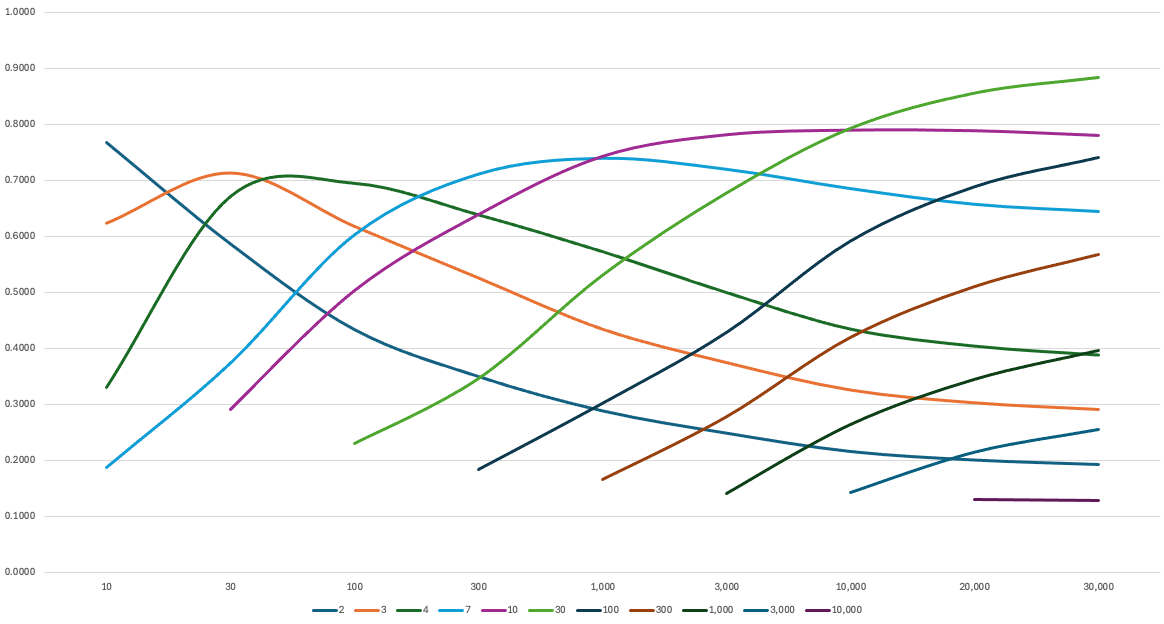
This behavior likely relates to an interesting property of high-dimensional geometry: as dimensionality increases, sphere packing becomes more efficient when the spheres are small relative to the unit sphere. This suggests that our observed upper bounds on C might still be conservative for very large numbers of concepts.

Practical Implications for Language Models

Let's consider three scenarios for the constant C:

1. C = 4: A conservative choice for random projections with Hadamard matrices
2. C = 1: A likely upper bound for optimized or emergent embeddings
3. C = 0.2: A value suggested by our experiments for very large spaces

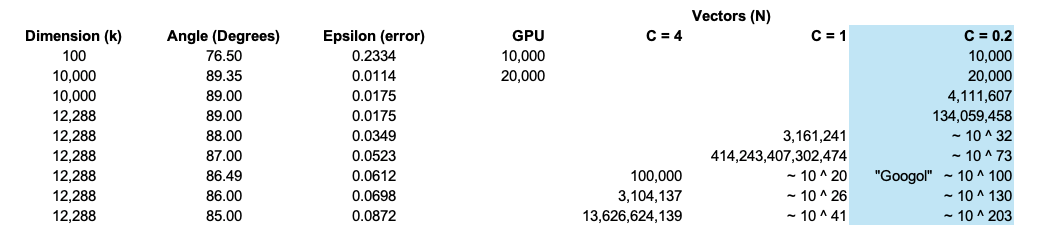
The implications of these geometric properties are staggering. Let's consider a simple way to estimate how many quasi-orthogonal vectors can fit in a k-dimensional space. If we define F as the degrees of freedom from orthogonality (90° - desired angle), we can approximate the number of vectors as:

Vectors ≈ 10^(k * F² / 1500)

where:

• k is the embedding dimension
• F is the degrees of "freedom" from orthogonality (e.g., F = 3 for 87° angles)

Applying this to GPT-3's 12,288-dimensional embedding space reveals its extraordinary capacity:

• At 89° (F = 1): approximately 10^8 vectors
• At 88° (F = 2): approximately 10^32 vectors
• At 87° (F = 3): approximately 10^73 vectors
• At 85° (F = 5): more than 10^200 vectors

To put this in perspective, even the conservative case of 86° angles provides capacity far exceeding the estimated number of atoms in the observable universe (~10^80). This helps explain how language models can maintain rich, nuanced relationships between millions of concepts while working in relatively modest embedding dimensions.

Practical Applications and Future Directions

The insights from this investigation have two major practical implications:

1. Efficient Dimensionality Reduction: The robustness of random projections, particularly when combined with Hadamard transformations (or BCH coding), provides a computationally efficient way to work with high-dimensional data. No complex optimization required – the mathematics of high-dimensional spaces does the heavy lifting for us.
2. Embedding Space Design: Understanding the true capacity of high-dimensional spaces helps explain how transformer models can maintain rich, nuanced representations of language in relatively compact embeddings. Concepts like "Canadian," "morose," "Hitchcockian," "handsome," "whimsical," and "Muppet-like" can all find their place in the geometry while preserving their subtle relationships to each other.

This research suggests that current embedding dimensions (1,000-20,000) provide more than adequate capacity for representing human knowledge and reasoning. The challenge lies not in the capacity of these spaces but in learning the optimal arrangement of concepts within them.

My code for Hadamard and optimized projections.

Conclusion

What began as an investigation into a subtle optimization issue has led us to a deeper appreciation of high-dimensional geometry and its role in modern machine learning. The Johnson-Lindenstrauss lemma, discovered in a different context nearly four decades ago, continues to provide insight into the foundations of how we can represent meaning in mathematical spaces.

I want to express my sincere gratitude to Grant Sanderson and the 3Blue1Brown channel. His work consistently inspires deeper exploration of mathematical concepts, and his openness to collaboration exemplifies the best aspects of the mathematical community. The opportunity to contribute to this discussion has been both an honor and a genuine pleasure.

I would also like to thank Suman Dev for his help in optimizing the GPU code.

This was enormously fun to research and write.

Nick Yoder

Further Reading

1. Sphere Packings, Lattices and Groups by Conway and Sloane
2. Database-friendly random projections: Johnson-Lindenstrauss with binary coins by Achlioptas
3. Hadamard Matrices, Sequences, and Block Designs by Seberry and Yamada